In the early 1960's using a simple system of equations to model convection
in the atmosphere, Edward Lorenz, an MIT meteorologist, ran headlong
into "sensitivity to initial conditions". In the process he sketched
the outlines of one of the first recognized
chaotic attractors
.
In Lorenz's meteorological computer modeling, he discovered the underlying
mechanism of
deterministic chaos
:
simply-formulated systems with only a few
variables can display highly complicated behavior that is unpredictable.
 Using his digital
computer, culling through reams of printed numbers and simple strip chart
plots of the variables, he saw that slight differences in one variable
had profound effects on the outcome of the whole system. This was one of
the first clear demonstrations of sensitive dependence on initial conditions.
Equally important Lorenz showed that this occurred in a simple, but physically
relevant model.
Using his digital
computer, culling through reams of printed numbers and simple strip chart
plots of the variables, he saw that slight differences in one variable
had profound effects on the outcome of the whole system. This was one of
the first clear demonstrations of sensitive dependence on initial conditions.
Equally important Lorenz showed that this occurred in a simple, but physically
relevant model.
He also appreciated that in real weather situations, this sensitivity
could mean the development of a front or pressure-system where there never
would have been one in previous models. In his famous 1963 paper Lorenz
picturesquely explains that a butterfly flapping its wings in Beijing could
affect the weather thousands of miles away some days later. This sensitivity
is now called the "butterfly effect".
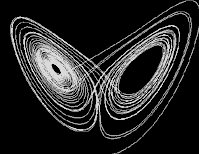
Here is a
Java
simulation
of the Butterfly Effect using the
chaotic attractor
that Lorenz discovered.
|